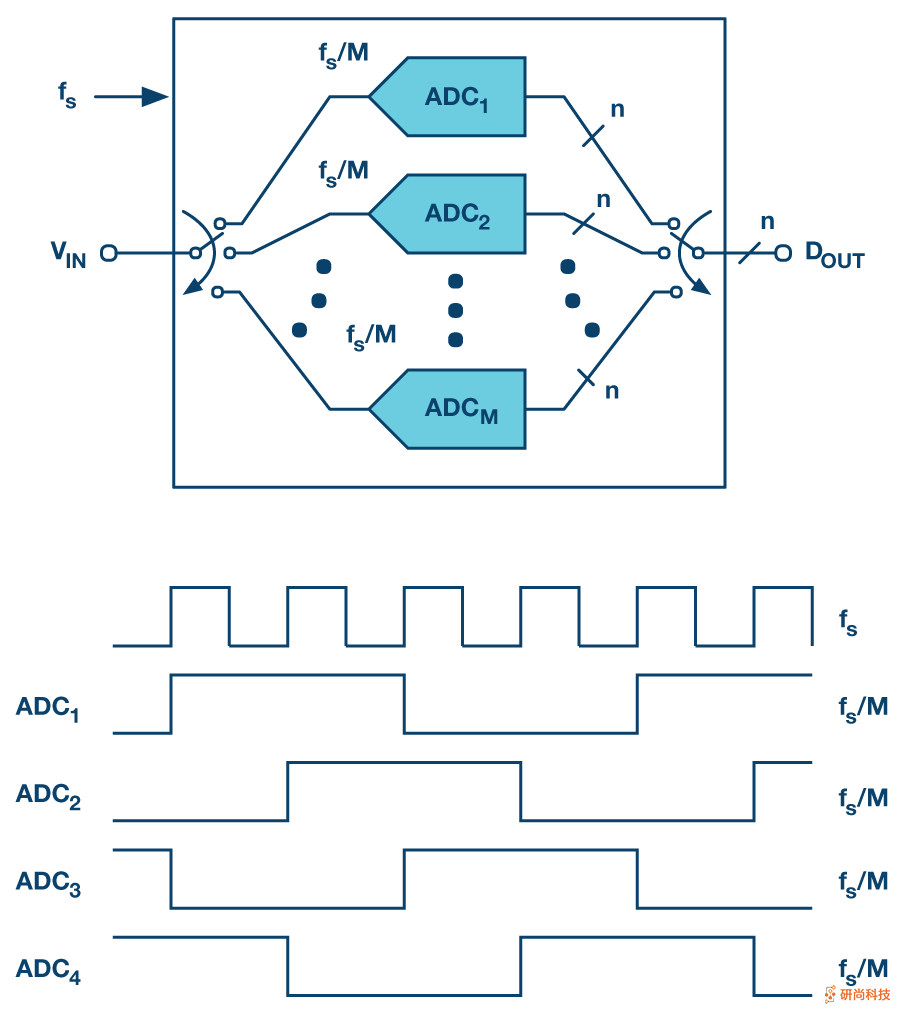
时间交织是一种技术，它允许使用多个相同的模数转换器（ADC）以比每个单独数据转换器的工作采样速率更快的速率处理常规采样数据序列。简单来说，时间交织（IL）包括对M个相同ADC的并行阵列进行时间复用，如图1所示，以实现更高的净采样率f s（采样周期T s = 1 / f s），甚至尽管阵列中的每个ADC实际上都以较低的f s / M速率采样（并转换）。因此，例如，通过交织四个10位/ 100 MSPS ADC，原则上可以实现10位/ 400 MSPS ADC。

为了更好地理解IL的原理，在图1中，由M个ADC采样了一个模拟输入V IN（t），并产生了一个组合的数字输出数据系列D OUT。ADC 1将首先对VIN（t 0）进行采样，并开始将其转换为n位数字表示。Ť小号秒后，ADC 2将采样V IN（吨0 + T小号），并开始将其转换成N位的数字表示。然后，Ť小号秒后，ADC 3将对V IN（t 0 + 2T s）进行采样，依此类推。在ADCM对V IN（t 0 +（M – 1）×T s）采样后，下一个采样周期开始于ADC1对V IN（t 0 + M×T s）采样，并且该轮播继续进行。

随着ADC的n位输出以与上述采样操作相同的顺序依次可用，这些数字n位字由同一图右侧所示的多路分解器收集。在此，获得重组数据输出序列D OUT（t 0 + L），D OUT（t 0 + L + T s），D OUT（t 0 + L + 2T s），...。L代表每个ADC的固定转换时间，此重组后的数据序列是采样率为f s的n位数据序列。因此，虽然单独的ADC中，常常被称为“通道”，是n比特的ADC在采样˚F小号/ M，在合奏包含在盒等效于在一个单一的n位ADC采样˚F小号，我们将其称为时间交错ADC（将其与通道区分开）。基本上，对输入进行切分并由阵列中的ADC进行单独处理，然后在输出端进行一致的重组，以形成输入V IN的高数据速率表示D OUT。

这种强大的技术并非没有实际挑战。当来自通道的M个数据流被数字组合在一起以重建原始输入信号V IN时，关键问题就显现出来了。如果我们查看D OUT的频谱，除了看到V IN 的数字表示和模数转换所引入的失真外，我们还将看到称为“交织杂散”（或“杂散”）的其他大量杂散内容。 IL杂散，简而言之，IL杂散都不具有多项式失真的特征，例如高阶信号谐波（第二，第三，等等），也没有量化或DNL错误的签名。IL伪影可以看作是时域固定模式噪声的一种形式，是由通道中的模拟损伤引起的，这些通道由于交织过程而被切分后的转换信号进行调制，最终出现在最终的数字化输出D OUT中。

让我们通过分析一个简单的示例来开始理解可能发生的情况。考虑具有频率为f IN的正弦输入V IN 的双向交错ADC的情况。假定ADC 1的增益为G 1，而ADC 2的增益为G2。在这样的双向IL ADC中，ADC 1和ADC 2将交替采样V IN。因此，如果ADC 1转换偶数样本，ADC 2转换奇数样本，则D OUT的所有偶数数据的振幅均由G 1设置，而D OUT的所有奇数数据均由G 1设置。D OUT 的振幅由G 2设定。那么D OUT不仅包含V IN 以及一些多项式失真，而且还经历了G 1和G 2的交替放大，就好像我们是用频率f s /的方波对V IN 进行幅度调制一样。 2。那就是将引入其他虚假内容的原因。具体来说，D OUT将包括频率为f s / 2 – f IN的“增益杂散” ，不幸的是，该杂散的频率跟踪输入fIN ，它位于交错ADC的第一个奈奎斯特频带内（即f s / 2之内），并且在所有其他奈奎斯特频带上也有别名。交错杂散的功率/幅度取决于两个增益G 1和G 2之间的净差。换句话说，这取决于增益误差失配。最后，它取决于输入V IN本身的大小。

如果输入不是简单的正弦波，但在实际应用中，它是一个整个频带受限的信号，那么“增益杂散”不仅仅是简单的不想要的音调，而是完整的按比例缩放的图像。带限输入信号本身，显示在奈奎斯特频带内。这在某种程度上抵消了交织提供的带宽增加的好处。

尽管在以上示例中，我们仅考虑了通道之间的增益误差失配，但其他损害也引入了交错杂散。失调失配（通道失调之间的差异）会在固定频率下引入音调（“失调杂散”），并且功率与失调失配成正比。当某些通道的采样早于或晚于预期顺序时，就会发生采样时间偏斜。这就引入了“定时杂散”，它与增益杂散处于相同的频率（并加在一起具有相同的幅度），但随着f IN的增加，功率越来越强 随着输入幅度的增加而增加。各个通道之间的带宽失配会在取决于f IN的频率上引入更多杂散内容，就像定时杂散一样，杂散功率会随着f IN本身而逐渐增强，而不仅仅是输入幅度。同样，在所有情况下，输出频谱退化的严重程度均不取决于通道损耗的绝对值（偏移，增益，时序，频带），而是取决于它们之间的相对失配/差异。

尽管一般的时间交织技术已经存在了几十年，但可以将IL杂散保持在最小的程度将其过去的适用性限制在低分辨率转换器上。但是，通道不匹配的校准和残余IL杂散成分的抑制方面的最新进展使今天可以实现完全集成的超高速12位，14位和16位IL ADC。

在这一点上，我们需要区分几类交织。在两个交错通道的情况下，我们通常指的是“乒乓”操作。然后，当我们指的是通道数量减少的情况（例如，三个通道到四个通道）或大量通道（例如四个以上）的情况时，我们可以区分“轻度交错”和“高度交错” ，通常分别是八个或更多。

乒乓（双向）交织

如图2（a）的框图所示，当我们仅交错两个通道以使净采样率翻倍时，我们将其称为“乒乓”。这是一个特别简单的案例，具有一些有趣且有用的功能。在这种情况下，1个内第一交错式ADC的奈奎斯特频带，所述交织杂散位于直流，在˚F小号/ 2，并在˚F小号/ 2 - ˚F IN。因此，如果输入信号V IN 是一个以f IN为中心的窄带信号，如图2（b）的第一个Nyquist输出频谱所示，则交织杂散将包括dc处的一个杂散杂散，另一个是失配杂散杂散。在f s/ 2，以及一个以f s / 2 – f IN 为中心的增益和定时杂散图像，看起来像是输入本身的缩放副本。

如图2（b）所示，如果输入信号V IN（f）完全限制在0和f s / 4之间，则交织杂散不会与数字化输入频率重叠。在这种情况下，一个坏消息是我们只能在奈奎斯特频带的一半进行数字化，即就像我们有一个时钟频率为f s / 2的单个信道一样，尽管我们仍然消耗至少两倍的功率。单个渠道。奈奎斯特频带上端的交错杂散图像可以在数字化后通过数字滤波来抑制，并且不需要校正模拟损伤。

不过，好消息是，由于乒乓ADC的时钟频率为f s，因此数字化输出受益于动态范围内的3 dB处理增益。而且，与使用时钟频率为f s / 2的单个ADC相比，乒乓ADC的抗混叠滤波器设计已经放宽了。

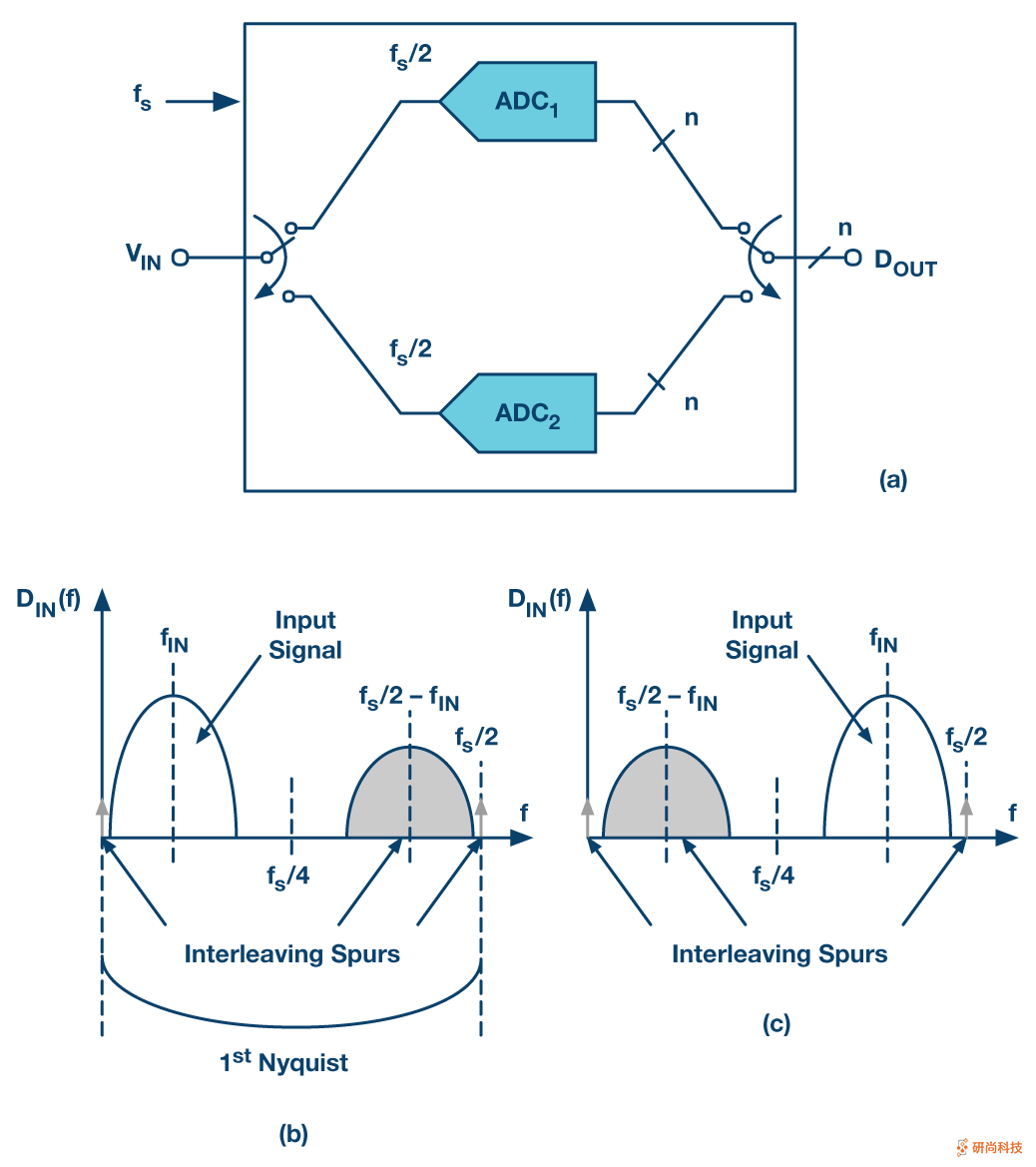
如果窄带信号位于第一奈奎斯特频带的上半部分，则可以重复所有相同的考虑，如图2（c）所示，因为交织图像杂散移到了奈奎斯特频带的下半部分。再一次，在数字化之后，可以通过滤波对增益和时序杂散进行数字抑制。

最后，输入信号的频率位置越过f s / 4线，输入信号和交织杂散将频率交叠，并且输入频谱被交织图像破坏。在这种情况下，无法恢复所需的输入信号，并且无法使用乒乓方案。当然，除非通道之间的匹配足够接近，以使得交织杂散含量对于应用而言可接受地低，或者除非采用校准来减少导致产生IL图像的原因，否则除非如此。

总而言之，频率规划和一些数字滤波甚至可以在存在信道失配的情况下，以乒乓方案恢复窄带数字化输入。与使用时钟频率为f s / 2的单个ADC相比，转换器的功耗大约增加了一倍，而乒乓方案提供了3 dB的处理增益，并放宽了抗混叠要求。

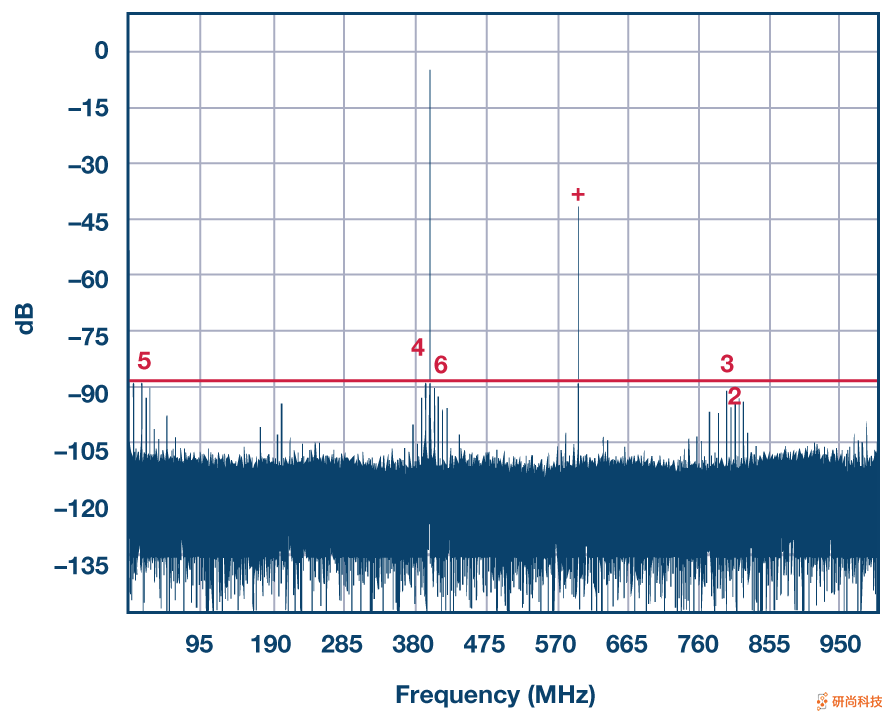
图3显示了一个乒乓球的示例，该乒乓球未对通道失配及其所引起的交错杂散进行任何校正。在这种情况下，双14位/ 1 GSPS ADC 的两个ADC交替采样单个正弦波，因此返回2 GSPS的单个组合输出数据流。当我们查看此乒乓球方案的输出频谱的第一个奈奎斯特频带（介于dc和1 GHz之间）时，我们可以看到输入音调，这是f IN = 400 MHz时左侧的强音调，还可以看到在f s / 2 – f IN = 2G / 2 – 400 M时，强烈的增益/时序不匹配杂散= 600 MHz。由于两个通道自身的失真以及其他损伤，我们还会看到许多其他音调，但是这些音调都在–90 dB线以下。

高阶交织 

当我们有两个以上的频道时，如上所述的频率规划不是很实用或没有吸引力。交错杂散的位置不能局限于奈奎斯特频带的一小部分。例如，考虑如图4（a）所示的四路交错ADC的情况。在这种情况下，失调失配会在dc，f s / 4和f s / 2处产生音调。增益和定时交织图像位于f s / 4 – f IN时，f s / 4 + f IN 和f s / 2 – f IN。交错ADC输出的频谱示例如图4（b）所示。可以清楚地看到，除非输入的带宽小于f s / 8，否则无论我们将f IN放置在什么位置，输入都会与一些交错的杂散重叠，并且如果输入是非常窄的-频带信号，我们不应该尝试使用宽带交错ADC将其数字化。

在这种情况下，我们需要最小化IL杂散功率，以获得完整的Nyquist和更清晰的频谱。为此，使用校准技术来补偿通道之间的不匹配。随着不匹配的影响得到纠正，所产生的IL杂散的功率会降低。SFDR和SNR都受益于这种杂散功率的降低。

补偿方法受到可以测量并最终纠正不匹配的精度的限制。为了进一步抑制残留杂散，使其超过通过校准获得的水平，可以间歇性地随机调整通道对输入进行采样的顺序。这样做时，由于未校准的失配，先前讨论的转换后的输入信号的调制效果从固定模式噪声变为伪随机噪声。结果，IL音调和不期望的周期性模式变成伪伪噪声样的内容，其与转换器量化本底噪声相加，并且导致不期望的虚假图像和音调的消失或至少扩散。在这种情况下，与IL杂散内容相关的功率会增加本底噪声的功率。因此，虽然失真会改善，但SNR可能会因添加到噪声中的IL杂散功率的数量而下降。SNDR（SINAD）基本上没有变化，因为它结合了失真，噪声和随机化。它只是将IL的影响从一个分量（失真）转移到另一个分量（噪声）。

让我们考虑一些交错ADC的示例。该ADC是一个12位/ 2.5 GSPS三路交错ADC。为了最小化交错杂散，对三个通道之间的失配进行了校准。输入接近1 GHz的输出频谱示例如图5（a）所示。在该光谱中，除了〜1GHz的输入灰度，能够看到通道2次和3次接近500兆赫的谐波失真和4个附近的基波的谐波失真。交织失配校准大大降低了交织杂散的功率，并且在整个频谱上可以看到一大组额外的残留小杂散音。

为了进一步减少这种残留的杂散内容，引入了信道随机化。添加第四个已校准的通道，然后通过以第四个通道间歇地交换一个交错的通道，以随机变化的顺序对四个通道进行三路交错。人们可以将其比作玩杂耍的人，他们在空中玩着三个“吃喝玩乐”，而第四个则经常被交换。这样，剩余的交织杂散功率被随机化并在本底噪声上散布。如图5（b）所示，在信道随机化之后，交织杂散几乎消失了，而噪声的功率却略有增加，从而使SNR降低了2 dB。当然，请注意，尽管图5（b）所示的第二个频谱明显更失真，但是混洗不会影响2nd，3 rd和4 th谐波，因为它们不是交错的杂散。

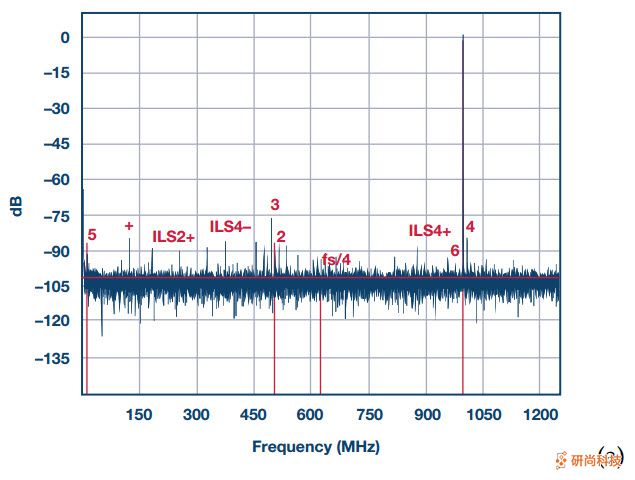
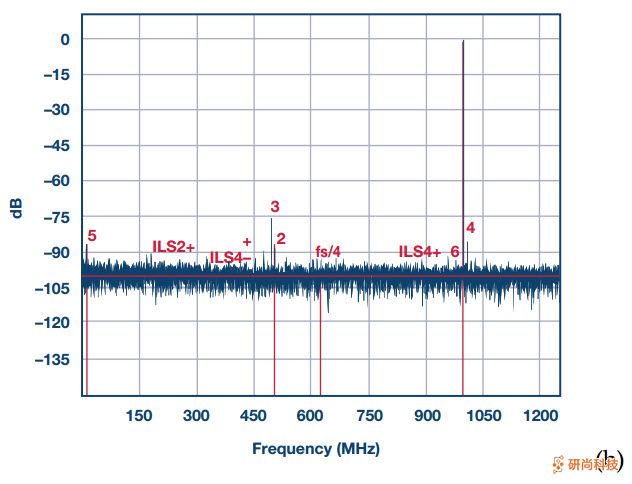
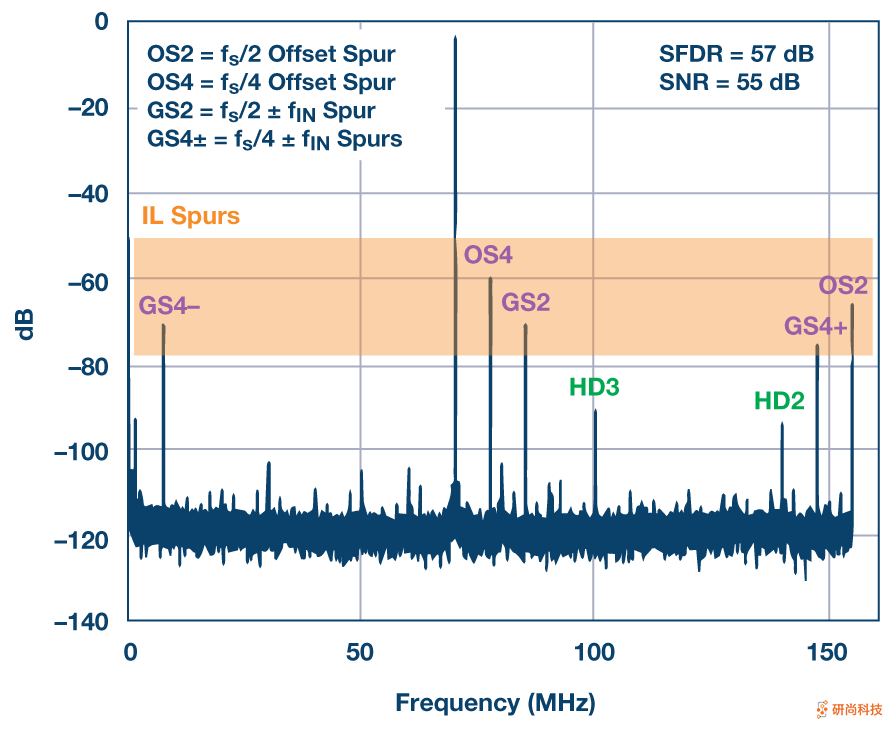
使用通道随机化的交错ADC的另一个示例如图6的频谱所示。这是四路交错16位/ 310 MSPS ADC AD9652的情况。在图6所示的情况下，四个通道以固定的顺序依次插入，而无需进行校准以减少通道不匹配。光谱清楚地示出的交织杂散在预测的频率位置和它们的大的功率远远大于2次大于第二和3次谐波，并且限制了无杂散动态范围只有57 dBc的。

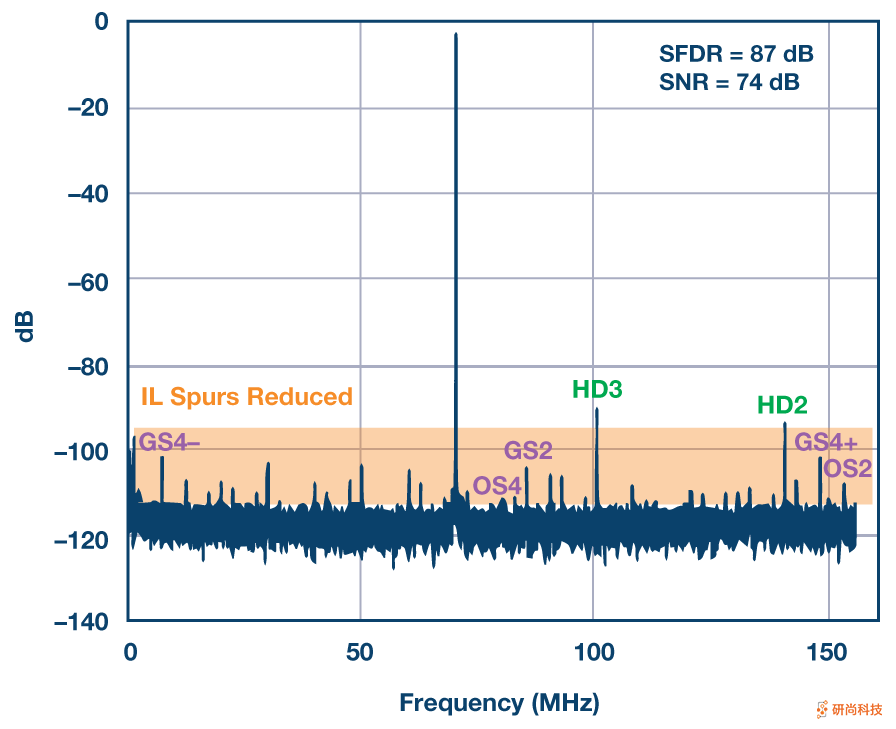
但是，如果对同一ADC进行前景校准以减少通道失配，则交错杂散的功率将大大降低，如图7所示。类似于前面的示例，通道谐波失真不受影响，但是通过通道失配校准，可大大降低交错杂散的功率。

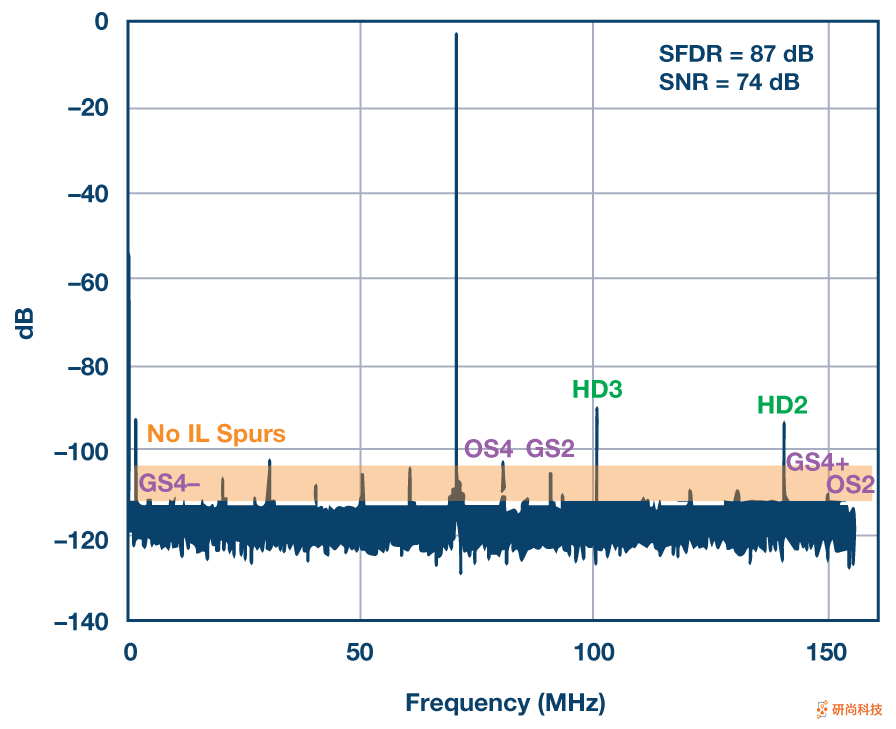
最后，可以通过如图8所示对通道顺序进行随机化来进一步提高图7中的光谱纯度。在这种情况下，随机化使用专有技术，该技术在间歇性地加扰四个通道的顺序时不需要多余的（5 th）通道被添加，因此节省了其相关的功率。从图8可以看出，在随机化之后，结果频谱上只剩下规则的谐波失真。

结论

时间交织是增加数据转换器带宽的强大技术。失配补偿以及通过随机化技术消除残留杂散内容的最新进展已实现了高速12位、14位和16位交错ADC的完全集成实现。

在输入信号受频带限制的情况下，例如在许多通信应用中，乒乓（双向）交织方法允许通过频率将不想要的交织杂散分配到感兴趣的输入频带之外规划。虚假内容然后可以进行数字过滤。尽管与非交织ADC相比，该方法消耗的功率大约是捕获相同无杂散输入带宽所需的IL采样率的一半，但功耗却是后者的两倍，但另一方面，它通过处理增益将动态范围提高了3 dB，并且还放宽了由于较高的IL采样率，ADC之前的抗混叠滤波器和屋顶滤波器的滚降。

当需要IL转换器的整个输入频带来捕获宽带输入信号时，较高阶的交织转换器是合适的。在这种情况下，校准和随机混洗允许交织失真以及杂散内容补偿和抵消。

研尚科技可提供的部分产品列表

• 音频编解码器： Codec、 ADC、 DAC、 音频功放、 硅麦、 耳放

• 射频器件： 定位芯片、 定位模块、 LNA、 无线射频芯片、 NFC

• 电源转换： 升压芯片、 降压芯片、 LDO、 背光驱动

• 电源管理： 锂电池充电管理、 锂电池保护、 QC快充协议、 OVP/OCP、 电压检测、 复位芯片、 PMU、 显示屏电源芯片、 MOSFET、 ESD

• 存储器： SDRAM、 DDR、 Flash、 EEPROM

• 马达驱动： 步进电机/无刷&有刷

• MCU微控制器： MCU、 指纹芯片、 加密芯片

• 无线通信： 5G&4G通讯模组、 NB-IoT模组

• 其它芯片： 运算放大器、 OSD